Analysis of the Influence of Interface Capture Center on the Static Characteristics of MOS Field Effect Transistor

The interface trapped state existing on the silicon-silicon dioxide interface affects the static characteristics of the MOS field effect transistor. When the interface state has a charge, the charge is included in the Qss as a fixed charge. This is done after section 1.2. But the charge of the interface state is related to the amount of electrons captured by the interface state, and the amount of charge is changing. Therefore, the existence of the interface state cannot be replaced by the existence of a fixed interface charge. At the same time, it must be considered that the silicon surface potential changes with the gate voltage and the drain voltage, and the interface state also undergoes charging and discharging.

This problem is first considered with a simple model. Let N1 be the areal density of the interface capture center,niIs the density of the trapping center of the carriers in the trapping channel, nm is the density of carriers in the channel. If τm is the lifetime of the carrier,is the average time the carrier is trapped by the trapping center. When the carrier lifetime is only determined by the trapping of the trapping center, the following formula can be established considering the conservation of carrier density:

The increase in the carrier density in the channel and the increase in the trapped carrier density caused by the increase in the gate voltage VGS are respectively set as d,then

Here, the space charge generated by the impurity ions of the substrate is also ignored.

Assuming that the channel width is W and the surface density of carriers is nm, the drain-source current IDS can be expressed as

Because the areal density of carriers is equal to the value nmo when the gate voltage is zero plus the induced carrier density, which is

In addition, the surface density of trapped carriers when the gate voltage is zero isBecause there are

and so

According to the definition of the usual pinch-off voltage Vp, there are

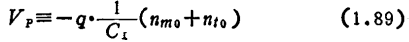
If defined by

The formula (1.89) can be written as

Substituting formula (1.91) into formula (1.83), when using steady state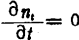conditions of. The value of  can be determined. But pay attention to the formula (1.83),Generallythe function. Thus, if S is the capture cross section of the capture center, sinceis the density of the empty trapping center, assuming that the average carrier velocity is, There are

Under the steady-state condition where the gate voltage is zero, due to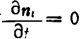,and so

Since the following relationship holds

The formula (1.83) can be written as

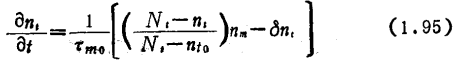
Substituting formula (1.92) into formula (1.95), the  is obtained as

where

From this, the leakage current can be obtained as

where

When VDS exceeds the VDSs defined by the following formula, it will be in a so-called pinch-off state.

The leakage current value when VDS is exactly equal to VDSS

Equation (1.104) differentiates VGs, and the transconductance gm can be calculated.

When the trapping center density is small, the carrier lifetime increases, soIncrease. Withcompared with items containingIf the item of can be ignored, there are

The pinch-off voltage Vp is

According to the formula (1.89), Vp can generally be written as

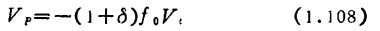
Now because, The formula (1.107) can be equivalent to the formula (1.108).

When the trapping center density is high, the carrier lifetime decreases, sodecrease, the leakage current at this time is

The pinch-off voltage Vp is

Due to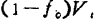

When the gate voltage is zero, it corresponds to the voltage of the empty trap level. When this empty trap level is filled, a current flows between the source and the drain.

The pinch-off voltage itself will vary withValue changes 9), such as

If it is very large or very small, the appropriate pinch-off voltage value can be used respectively. Except near the threshold value, the static characteristics can be expressed in the same form as the simplest case formula 1.16).

In the above derivation, it is assumed that the trapping energy levels of the interface all have the same trapping cross section, and the density of states distribution of the trapping energy levels is not considered. But we know that the interface state density measured by experiment has a rather complicated distribution. Calculations that take this interface state density distribution into account must be calculated numerically. Interface state density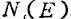One of the numerical calculation results of static characteristics when the following three distributions are taken is shown in Figure 1.1510).

The characteristics near the threshold fully reflect the distribution of the interface state density. As it moves away from the threshold, it should be interpreted as a difference in pinch-off voltage, which causes the characteristics to shift.

Contact: Mr. Zou

Contact number: 0755-83888366-8022

Mobile phone: 18123972950

QQ: 2880195519

Contact Address: 5C1, CD Block, Tianji Building, Tianan Digital City, Chegongmiao, Futian District, Shenzhen

Please search WeChat official account: "KIA Semiconductor" or scan the following picture to "Follow" official WeChat official account

Please "follow" the official WeChat account: provide MOS tube technical assistance