The relationship between carrier mobility and gate voltage in MOSFET channel

So far, the carrier mobility μch in the channel has not been involved too much, and it is regarded as a constant. However, the value of the carrier mobility in the channel is smaller than the value μB measured on a bulk silicon crystal, and the measured value varies with the gate voltage and the drain voltage. The relationship between μch and the gate voltage and the smaller value of μch than the crystal body are closely related to these two points. Therefore, it is necessary to discuss this issue.

It is known that not only the mobility of carriers in the inversion layer of the semiconductor surface, but also the mobility observed in the thin film is smaller than the mobility measured in bulk crystals. It can be considered that the common cause of the two is surface scattering. However, this kind of surface scattering is like the specular reflection shown in Figure 1.10(a); since the carrier momentum along the surface direction does not change, the conduction phenomenon along the surface direction does not change due to the existence of the surface. , So the carrier mobility does not change due to the presence of the surface. In addition, as shown in Figure 1.10(b), if there is no momentum change along the surface direction, the carrier mobility will not change due to the presence of the surface.

The reflection shown in Figure 1.10(b) is generated everywhere on the surface because the unevenness of the surface must be randomly distributed. If the surface roughness and the wavelength of the spatial distribution are sufficiently smaller than the wavelength of the incident carrier, the incident carrier is not affected by the roughness. What happens is specular reflection. Carrier mobility in the channel. If it is long enough compared with the wavelength of the incident carrier, it cannot be said to be a uniform surface from a macroscopic point of view, and the roughness of approximately the same order as the wavelength of the incident electron must be considered. For the silicon surface inversion layer, the wavelength of incident electrons is on the order of tens of angstroms, and it can be considered that there is a surface roughness of this order. When there is carrier diffuse scattering, the current equation can be obtained by solving the following Boltzmann transport equation under diffuse scattering boundary conditions, and then the carrier mobility can be calculated from the current equation

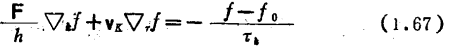
Where

F is the force added to the carrier

h=h/2π, h is Planck's constant

⊿k ⊿r are the differential operators of k and r respectively. k is the wave vector of the electron. r is the position vector of the electron

f is the distribution function of electrons

fo is the distribution function of electrons in thermal equilibrium

vk is the electron velocity with wave vector k

τk is the relaxation time of scattering

For the silicon surface inversion layer, as shown in Figure 1.11, take the silicon surface as the origin of the z-axis, and take the positive value of z toward the direction of the silicon body. When the boundary condition is z→∞, although f→fo, Indicates that there is a problem with the expression method of diffuse scattering at z=0. Carrier mobility in the channel. The commonly used method is to assume that no matter what momentum the carriers have before they are incident, the momentum distribution after diffuse scattering is completely independent of that before incident.

Therefore, it is assumed that the distribution of carriers after diffuse scattering takes the same distribution as the thermal equilibrium, when

, Can be considered

When the effective mass of electronics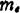it is a scalar, and τk has nothing to do with k, and when it is a constant τ, the Boltzmann transport equation can be solved. Now suppose the electric field along the surface is  to calculate the current, There are

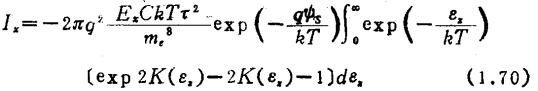
Where

q is the carrier charge

C as the reasondefined constant

ψ is the electrostatic potential s is the surface potential

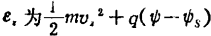
, Ez is the electric field intensity in the z direction.

In order to integrate the formula (1.70) analytically, Ez should be a constant Ezs independent of z, at this time

where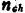is the carrier surface density in the surface inversion layer

From the formula (1.71), the analytical formula 8) of the mobility can be obtained,

If you use a graph to show the constant electric field in Figure 1.12, that is, the approximate curve of the triangular potential. It can be seen from the figure that as the gate voltage increases, the mobility of carriers in the channel decreases. However, the approximation of Ez to a constant value is not ideal. As shown in Figure 1.12, it is quite different from the result calculated by assuming the parabolic shape of the electric potential distribution. This point should be noted 7).

From a physical point of view, there are fundamental problems with the aforementioned theory of surface scattering. That is to say, when the inversion layer is formed on the silicon surface in the normal operating state of the MOS field effect transistor, even if the thickness of the space charge layer is on the order of microns, the thickness of the inversion layer is only tens ofTo 100 of magnitude. On the other hand, the wavelength of electrons in the inversion layer is also of the same magnitude. As shown in Figure 1.13, a standing wave of electrons may be formed between the potential barrier between silicon and silicon dioxide and the lower end of the conduction band or the upper end of the valence band in silicon. Therefore, the electrons in the inversion layer cannot take continuous energy values and should take discrete values. This phenomenon is called surface quantization.

When this quantization effect is significant, electrons cannot move in the z direction perpendicular to the surface of the semiconductor, and the electrons on the surface have only degrees of freedom to move along the surface of the semiconductor, and the electrons are in a two-dimensional state. Carrier mobility in the channel. Therefore, it is impossible to imagine the phenomenon that electrons bounce back after colliding with the barrier at the interface of silicon and silicon dioxide film, so the aforementioned surface scattering idea has substantial problems.

then, the relationship with the gate voltage is

Then there is

thus

This is the relational formula corresponding to formula (1.15).

There are theories that take into account the various scattering mechanisms of the electron mobility in the quantized state of the surface, but it is difficult to say that these theories have a thorough understanding of the scattering mechanism.

Contact: Mr. Zou

Contact number: 0755-83888366-8022

Mobile phone: 18123972950

QQ: 2880195519

Contact Address: 5C1, Block CD, Tianji Building, Tianan Digital City, Chegongmiao, Futian District, Shenzhen

Please search WeChat official account: "KIA Semiconductor" or scan the following picture to "Follow" official WeChat official account

Please "follow" the official WeChat account: provide MOS tube technical assistance