MOS tube integrated filter overview example and basic detailed explanation

Filters have a wide range of applications in various fields such as communication systems, industrial control, instrumentation, data detection and processing. From the perspective of historical development, the early filters were usually implemented with passive resistors, inductors, capacitors and other components. Such filters are usually called RLC filters. However, in low frequency applications, the inductance of the RLC filter has problems in terms of electrical loss, noise, and volume. Therefore, in the early 1970s, people began to use RC active filters composed of integrated operational amplifiers, resistors, capacitors and other components. Because of its excellent performance and easy manufacture, RC active filters are widely used. In recent years, due to the birth of MOS integrated operational amplifiers with low power consumption and high input impedance, people have begun to widely use RC active filters of MOS integrated operational amplifiers. Overview of MOS tube integrated filter. At the same time, due to the increasingly perfect MOS technology, an integrated switched capacitor filter composed of MOS operational amplifiers, MOS capacitors and MOS analog switches has developed rapidly in recent years. In the audio field, this switched capacitor filter is gradually Replace RLC passive filter and RC active filter. This section introduces the design methods of RC active filters and integrated switched capacitor filters composed of integrated operational amplifiers, and gives the design formulas, diagrams and practical circuit structures of the filters for engineering design. In order to enable readers to master the design method of integrated filters, this chapter gives the design steps and examples of practical integrated filters.

The filter can usually be regarded as a two-port linear network, which can transmit signals in a certain frequency range and block signals in a certain frequency range. Overview of MOS tube integrated filter. The frequency range that allows the signal to pass is called the pass band, and the frequency range that prevents the signal from passing is called the stop band. According to the position of the pass band and the stop band in the frequency domain, the filter is divided into low pass, high pass, band pass and band stop. Four types.

The low-pass filter passes low-frequency signals while attenuating or suppressing high-frequency signals. The amplitude response of the ideal low-pass filter is shown by the dotted line in Figure 5.1-1a. The passband gain is 1 (or a constant), the passband bandwidth is image.png, and the stopband is attenuated to zero, so it is ideal The frequency response is

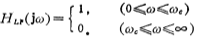
The ideal low-pass amplitude response is impossible to achieve, but the following transfer function can be used to approximate the ideal characteristics,

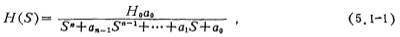
where is a suitably chosen constant. The above formula represents an n-th order all-pole approximation formula. The low-pass filter realized by this formula is called an n-th order all-pole low-pass filter. The larger the n, the closer the amplitude-frequency response of the actual low-pass filter is to the ideal The amplitude-frequency response of the low-pass filter. The achievable amplitude and whisker response that is close to the ideal characteristic is shown as the solid line in Figure 5.1-1a. The gain of the low-pass filter is the value of the transfer function when S=0. In the formula (5.1-1), the gain is Ho, If Ho takes 1, the gain is 1.

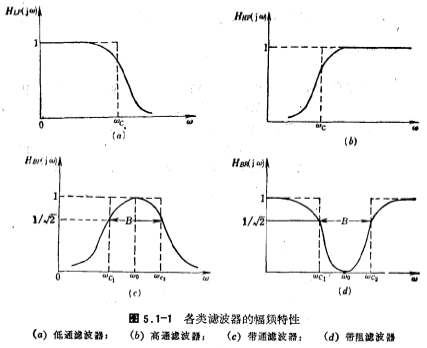
The high-pass filter passes high-frequency signals while attenuating low-frequency signals. The ideal high-pass amplitude-frequency response is shown by the dotted line in Figure 5.1-1b, and the relationship is

The achievable amplitude-frequency response that is close to the ideal characteristic is shown by the solid line. In order to obtain the transfer function of the high-pass filter, it is only necessary to substitute 1/S for S in the transfer function of the low-pass filter. Therefore, the transfer function of the high-pass filter can be obtained by transforming the transfer function of the low-pass filter.

The band pass filter passes the center frequency as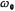, The bandwidth is the signal of the frequency band of B, and the signal outside the frequency band of B is attenuated. ratio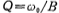, Called the quality factor of the filter, can be used to measure the selectivity of the filter. The gain of a bandpass filter is defined as the transfer function at the center frequency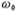the amplitude at the place. Overview of MOS tube integrated filter. The amplitude-frequency response of an ideal band-pass filter is shown in Figure 5.1-1c, and the relationship is

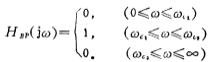
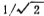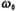An achievable amplitude-frequency response similar to the ideal characteristic is shown by the solid line. For the achievable approximate response, the cut-off whisker rate, the amplitude drops to the maximumthe frequency at and the bandwidth is defined as,center frequencyusually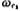andthe geometric mean of。

Like the high-pass filter, the transfer function of the band-pass filter can also be obtained by transforming the transfer function of the low-pass filter. Band stop filter (also called notch filter) is a kind of filter that passes all other frequency signals except one frequency. The amplitude-frequency response of the band-stop filter is shown in Figure 5.1-1d, where the dashed line represents the ideal amplitude-frequency response, and the solid line represents the approximate ideal characteristic and achievable amplitude-frequency response. Overview of MOS tube integrated filter. The frequency band to be blocked is 0. Is the center, and its width is B. Same as the band pass filter, the definition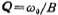. Therefore, high Q means a narrow stop band, and low Q means a stop bandwidth. In Figure 5.1-1(d)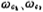, Is the cut-off rate of the stop band filter,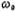usuallythe geometric mean of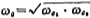. The amplitude-frequency relationship of an ideal band-stop filter is

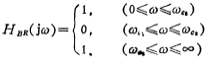
For the actual band stop filter, the cut-off frequency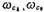the amplitude of the maximum amplitude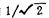(Suppose the maximum gain is 1), and its bandwidth is。

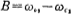Like the high-pass and band-pass filters, the transfer function of the band-stop filter can be obtained by transforming the transfer function of the low-pass filter.

Contact: Mr. Zou

Contact number: 0755-83888366-8022

Mobile phone: 18123972950

QQ: 2880195519

Contact Address: 5C1, Block CD, Tianji Building, Tianan Digital City, Chegongmiao, Futian District, Shenzhen

Please search WeChat official account: "KIA Semiconductor" or scan the following picture to "Follow" official WeChat official account

Please "follow" the official WeChat account: provide MOS tube technical assistance